Transformation in Computer Graphics
Spatial transformation
Generate a 3D grid of evenly spaced points:
def plot3d(pts, res=None, x=None, y=None, z=None):
plt.figure()
ax = plt.axes(projection='3d')
ax.scatter3D(pts[:, 0], pts[:, 1], pts[:, 2], facecolor=(0,0,0,0), edgecolor='b', linewidth=0.5)
if res is not None:
ax.scatter3D(res[:, 0], res[:, 1], res[:, 2], facecolor=(0,0,0,0), edgecolor='r', linewidth=0.5)
if x is not None:
ax.set_xlim3d(x[0], x[1])
if y is not None:
ax.set_ylim3d(y[0], y[1])
if z is not None:
ax.set_zlim3d(z[0], z[1])
pts = np.array(np.meshgrid(np.arange(21), np.arange(21), np.arange(5))).T.reshape(-1, 3)
plot3d(pts, x=[0,20], y=[0,20], z=[0,20])
Write a function rigid_transform(theta, omega, phi, p, q, r) that returns the matrix (in homogenous coordinates) of the rigid transform corresponding to:
- rotation of angle theta around the x-axis;
- rotation of angle omega around the y-axis;
- rotation of angle phi around the z-axis;
- translation of vector \(\mathbb{t}=(p, q, r)\). Then test our function on the 3D point cloud:
def rigid_transform(theta=0, omega=0, phi=0, p=0, q=0, r=0):
M = np.identity(4)
M[:3, 3] = [p, q, r]
angles = np.deg2rad([theta, omega, phi])
sin = np.sin(angles[0]); cos = np.cos(angles[0])
R = np.array([[1, 0, 0], [0, cos, -sin], [0, sin, cos]])
M[:3, :3] = M[:3, :3].dot(R)
sin = np.sin(angles[1]); cos = np.cos(angles[1])
R = np.array([[cos, 0, sin], [0, 1, 0], [-sin, 0, cos]])
M[:3, :3] = M[:3, :3].dot(R)
sin = np.sin(angles[2]); cos = np.cos(angles[2])
R = np.array([[cos, -sin, 0], [sin, cos, 0], [0, 0, 1]])
M[:3, :3] = M[:3, :3].dot(R)
return M
def warpAffine(p, m):
return m.dot(np.hstack((p, np.ones((p.shape[0], 1)))).T).T[:, :-1]
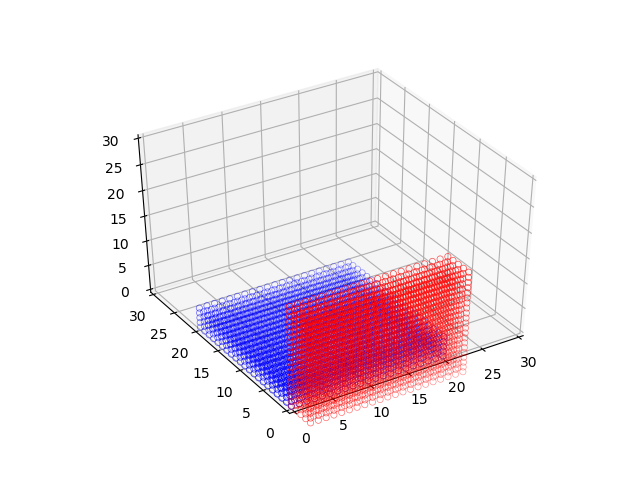
rigid_transform(theta=90, omega=0, phi=0, p=0, q=0, r=0)
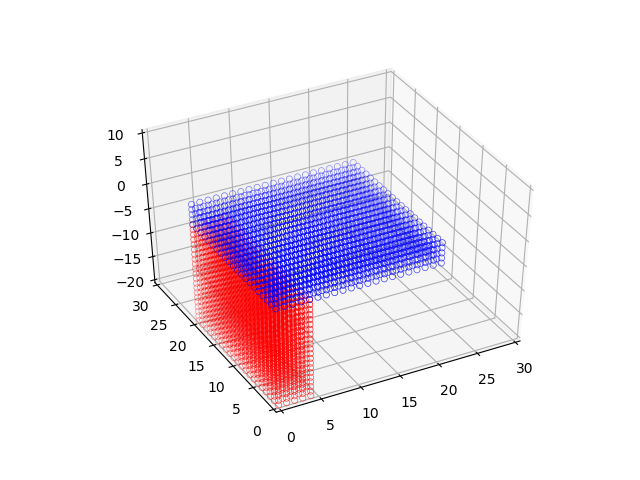
rigid_transform(theta=0, omega=90, phi=0, p=0, q=0, r=0)
rigid_transform(theta=0, omega=, phi=90, p=0, q=0, r=0)

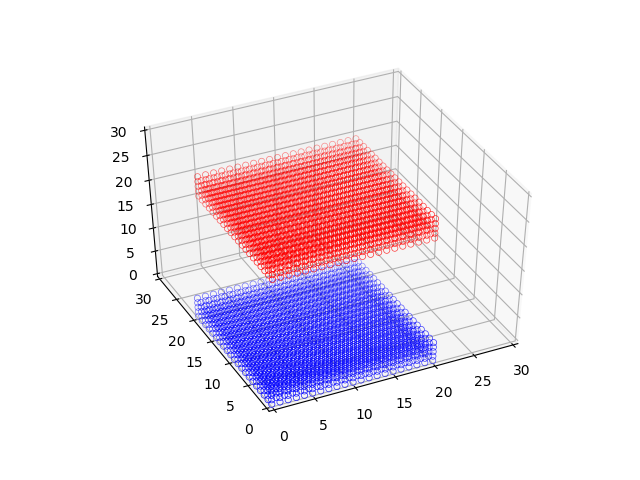
rigid_transform(theta=0, omega=0, phi=0, p=5, q=10, r=15)
Write a function affine_transform(s, theta, omega, phi, p, q, r) that does the same as above and adds a scaling factor \(s\).
def affine_transform(s=1, theta=0, omega=0, phi=0, p=0, q=0, r=0):
M = rigid_transform(theta, omega, phi, p, q, r)
return M.dot(np.diag([s]*3 + [1]))
affine_transform(s=0.5, theta=90, omega=0, phi=20, p=-10, q=-5, r=0)
Given the 3 following matrices \(M1, M2, M3\):
M1 = np.array([[0.9045, -0.3847, -0.1840, 10.0000],
[0.2939, 0.8750, -0.3847, 10.0000],
[0.3090, 0.2939, 0.9045, 10.0000],
[0, 0, 0, 1.0000]])
M2 = np.array([[-0.0000, -0.2598, 0.1500, -3.0000],
[0.0000, -0.1500, -0.2598, 1.5000],
[0.3000, -0.0000, 0.0000, 0],
[0, 0, 0, 1.0000]])
M3 = np.array([[0.7182, -.3727, -0.5660, 1.8115],
[-1.9236, -4.6556, -2.5512, 0.2873],
[-0.6426, -1.7985, -1.6283, 0.7404],
[0, 0, 0, 1.0000]])
Determine the type of transformation corresponding to each matrix:
def decompose_matrix(matrix):
M = np.array(matrix, dtype='float64', copy=True).T
angles = np.zeros(3)
translate = M[3, :3].copy()
M[3, :3] = 0.
row = M[:3, :3].copy()
scale = np.linalg.norm(row[0])
row /= scale
if np.dot(row[0], np.cross(row[1], row[2])) < 0:
scale = np.negative(scale)
row = np.negative(row)
angles[1] = np.arcsin(-row[0, 2])
if np.cos(angles[1]):
angles[0] = np.arctan2(row[1, 2], row[2, 2])
angles[2] = np.arctan2(row[0, 1], row[0, 0])
else:
angles[0] = np.arctan2(-row[2, 1], row[1, 1])
angles[2] = 0.0
return scale, np.rad2deg(angles), translate
Order: scale, rotation, translation
M1:
0.9999892299420029
[ 18.00058068 -17.99917668 18.00058068]
[10. 10. 10.]
M2:
0.3
[ -0. -90. 180.]
[-3. 1.5 0. ]
M3:
2.1515071368694083
[-132.15660825 17.37799903 -69.52625654]
[1.8115 0.2873 0.7404]