Image Registration
Joint histogram
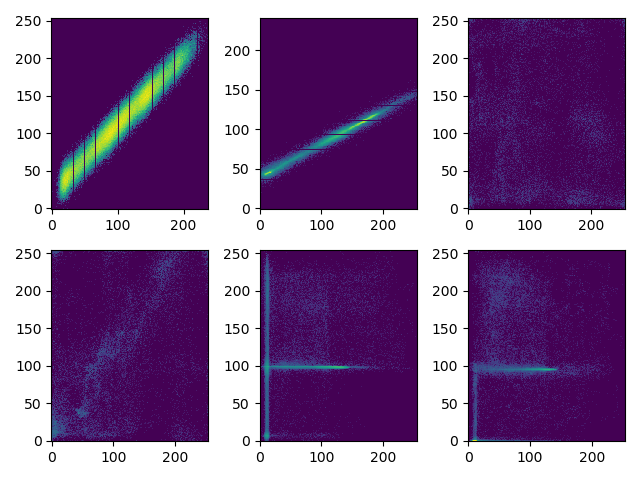
A python function JointHist(I, J, bin) which calculates the joint histogram of two images of the same size. For images of size \(n\times p\), verify \(\sum_{i,j}H_{I,J}(i,j) = n\times p\). Calculate and show the joint histogram of different pairs of images given here (I1, J1, I2, J2, etc.). Use the logarithmic scale to visualize joint hist:
def JointHist(I=None, J=None, bins=None, normed=False):
sample = np.asarray([I.ravel(), J.ravel()]).T
D = 2
nbin = np.empty(D, int)
edges = D*[None]
if bins is None:
bins = [I.max(), J.max()]
for i in range(D):
if np.ndim(bins[i]) == 0:
a = sample[:, i]
if a.size == 0:
smin, smax = 0, 1
else:
smin, smax = a.min(), a.max()
if smin == smax:
smin -= 0.5
smax += 0.5
edges[i] = np.linspace(smin, smax, bins[i] + 1)
elif np.ndim(bins[i]) == 1:
edges[i] = np.asarray(bins[i])
nbin[i] = len(edges[i]) + 1
Ncount = tuple(np.searchsorted(edges[i], sample[:, i], side='right') for i in range(D))
for i in range(D):
on_edge = sample[:, i] == edges[i][-1]
Ncount[i][on_edge] -= 1
xy = np.ravel_multi_index(Ncount, nbin)
hist = np.bincount(xy, minlength=nbin.prod())
hist = hist.reshape(nbin)
hist = hist.astype(float, casting='safe')
core = D*(slice(1, -1),)
hist = hist[core]
if normed:
s = hist.sum()
hist /= s
return hist
Similarity criteria
Write a python function SSD(I, J) that calculates the sum squared difference between two images I and J of the same size.
def SSD(I, J):
diff = (I.ravel() - J.ravel()).astype('uint64')
return np.dot(diff, diff)
Write a python function corr(I, J) that calculates the pearson correlation coefficient between two images of the same size.
def corr(I, J):
I = I.ravel()
J = J.ravel()
dtype = type(1.0 + I[0] + J[0])
Imean = I.mean(dtype=dtype)
Jmean = J.mean(dtype=dtype)
Im = I.astype(dtype) - Imean
Jm = J.astype(dtype) - Jmean
normIm = np.linalg.norm(Im)
normJm = np.linalg.norm(Jm)
r = np.dot(Im/normIm, Jm/normJm)
r = max(min(r, 1.0), -1.0)
return r
Write a function MI(I, J) that calculates the mutual information between two images of the same size.
def MI(I, J):
Hij = JointHist(I, J)
nzi, nzj = np.nonzero(Hij)
nz_val = Hij[nzi, nzj]
Hij_sum = Hij.sum()
pi = Hij.sum(axis=1).ravel()
pj = Hij.sum(axis=0).ravel()
log_Hij_nm = np.log(nz_val)
Hij_nm = nz_val / Hij_sum
outer = pi.take(nzi).astype('int64', copy=False) * pj.take(nzj).astype('int64', copy=False)
log_outer = -np.log(outer) + np.log(pi.sum()) + np.log(pj.sum())
mi = Hij_nm * (log_Hij_nm - np.log(Hij_sum)) + Hij_nm * log_outer
return np.clip(mi.sum(), 0.0, None)
Simple 2D registration
Write a function translation(I, p, q) that returns a new image corresponding to image I translated by vector \(\mathbb{t}=(p,q)\) (\(p, q\) may be floats), use existing interpolation functions in scipy.
from scipy.interpolate import interp2d
def translation(I, p ,q):
x, y = np.range(I.shape[0]), np.range(I.shape[1])
f = interp2d(x+q, y+p, I, kind='cubic', fill_value=0)
return f(x, y)
translation(I1, 20, 50)
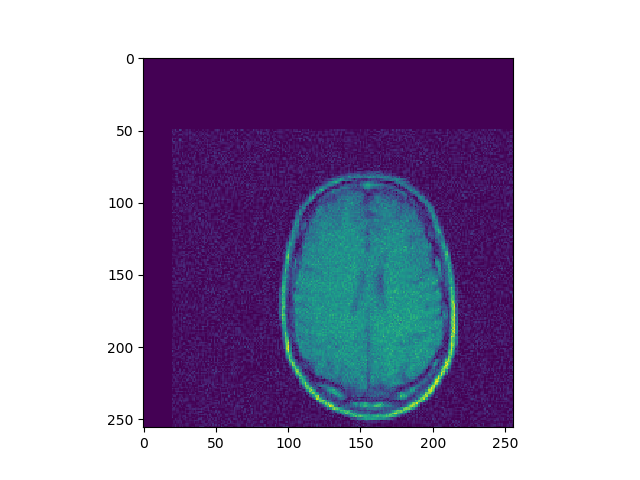
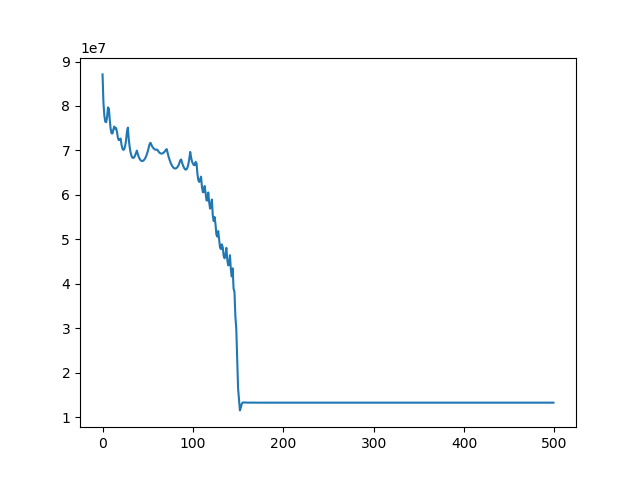
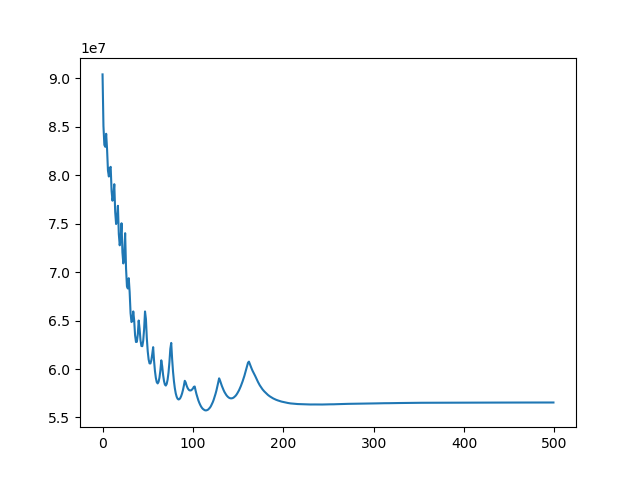
Implement 2D registration minimizing SSD and considering only translation. Search for the alignment, and save the SSD for each iteration. Then test the function on the 3 different translations for image BrainMRI_1.png (BrainMRI_2, 3, 4). Show the registration obtained and the SSD curve as a function of iteration.
def search(I, J, lr=1e-7, iters=100):
u = np.zeros(2)
cost_history = np.zeros(iters)
x, y = np.arrange(I.shape[0]), np.arrange(I.shape[1])
vu = np.zeros(2)
for itr in range(iters):
curr = translation(J, u[0], u[1])
gy, gx = np.gradient(curr)
dx = -((curr - I)) * gx).sum() * 2
dy = -((curr - I)) * gy).sum() * 2
du = np.array([dx, dy])
cu = lr * du
u -= cu
cost_history[itr] = SSD(curr, I)
return u, cost_history
u, ch = search(I1, I2, lr=1e-7, iters=500)
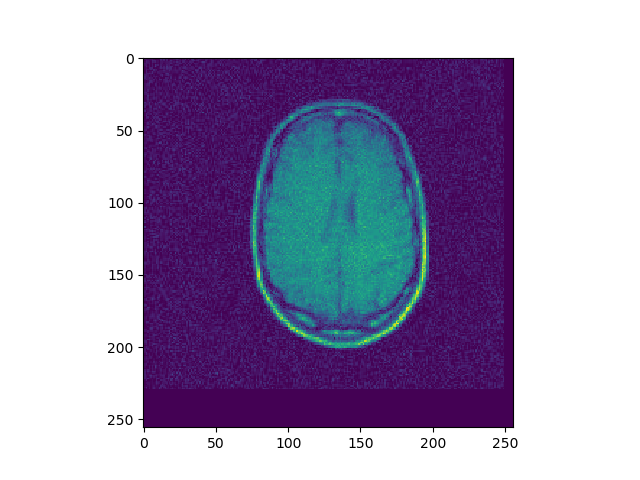
u, ch = search(I1, I3, lr=1e-7, iters=500)
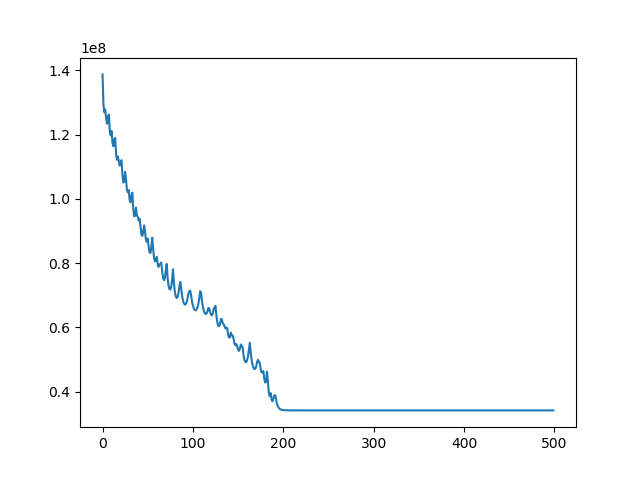
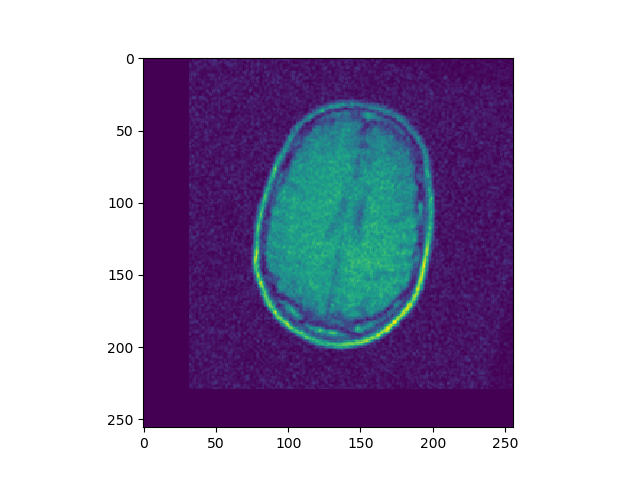
u, ch = search(I1, I4, lr=1e-7, iters=500)
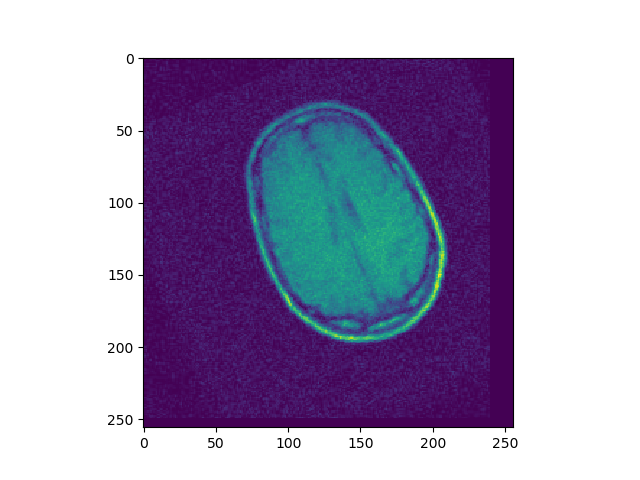
Write a function rotation(I, theta) which returns an image I’ that has been rotated by an angle theta, around the top left of the image. Create a grid corresponding to the image, rotate the grid, and interpolate using scipy interpolation functions.
from scipy.interpolate import interpn
def rotation(I, theta):
xs, ys = np.arange(I.shape[0]), np.arange(I.shape[1])
theta = np.def2rad(theta)
c, s = np.cos(theta), np.sin(theta)
m = np.array([[c, -s], [s, c]])
pts = np.array(np.meshgrid(xs, ys)).T.reshape(-1, 2)
out = m.dot(pts.T).T.reshape(I.shape[0], I.shape[1], 2)
return interpn((xs, ys), I, out, bounds_error=False, fill_value=0)
rotation(I1, 15)
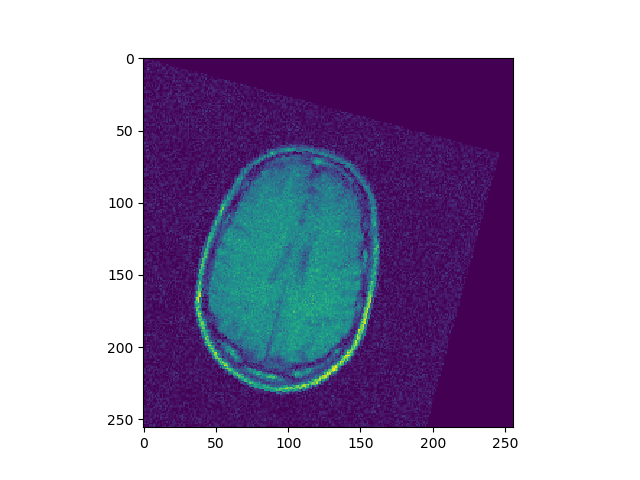
Implement 2D registration minimizing SSD and considering only rotations. For each iteration, save the SSD. Test this function on the 3 differently rotated images. Visualize the obtained registrations and SSD curve.
def search(I, J, lr=1e-7, iters=100):
t = 0
cost_history = np.zeros(iters)
x, y = np.arrange(I.shape[0]), np.arrange(I.shape[1])
vt = 0
for itr in range(iters):
curr = rotation(J, t)
c, s = np.cos(np.deg2rad(t)), np.sin(np.deg2rad(t))
gy, gx = np.gradient(curr)
dt = -2 * ((curr - I) * (gy*(x*c-y*s) - gx*(x*s+y*c))).sum()
ct = lr * dt
t -= ct
cost_history[itr] = SSD(curr, I)
return t, cost_history
t, ch = register(I1, I2, lr=1e-10, iters=1000)
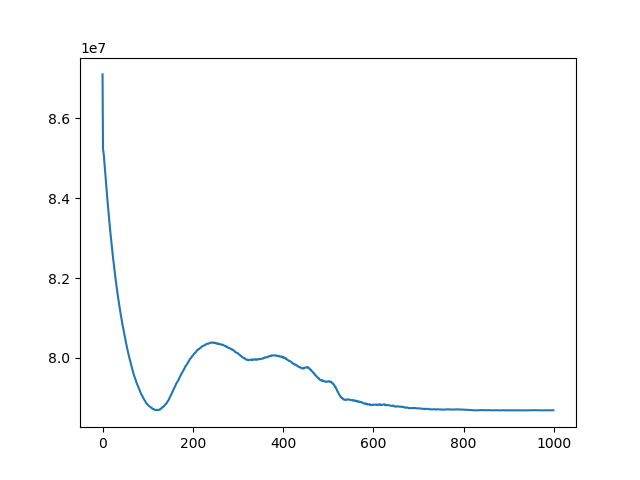
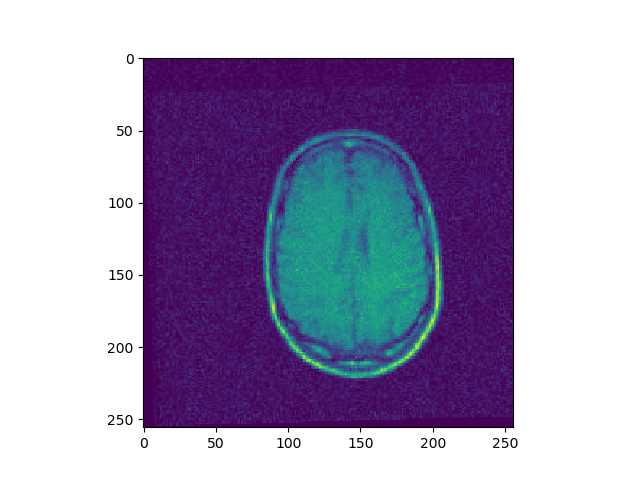
t, ch = register(I1, I3, lr=1e-10, iters=500)
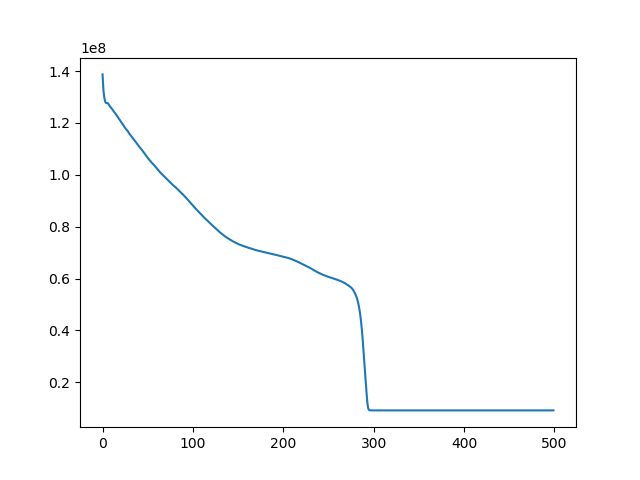
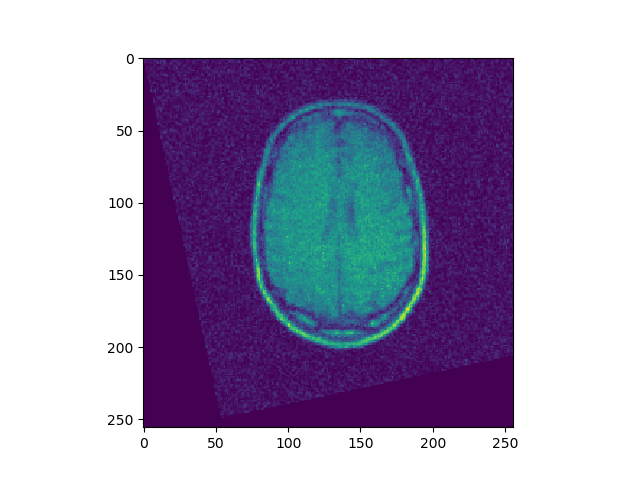
t, ch = register(I1, I4, lr=1e-10, iters=1000)
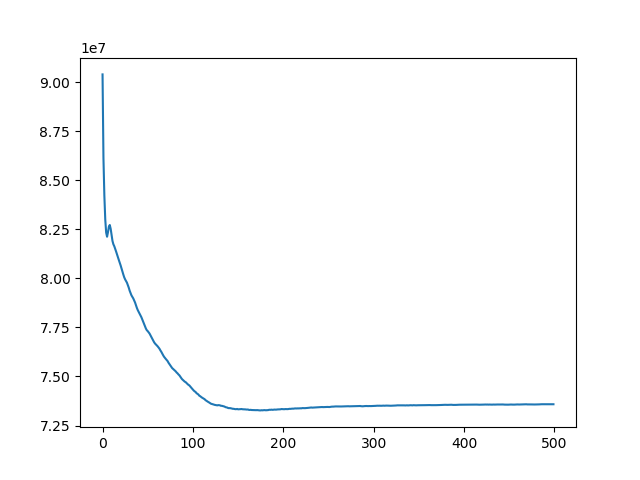
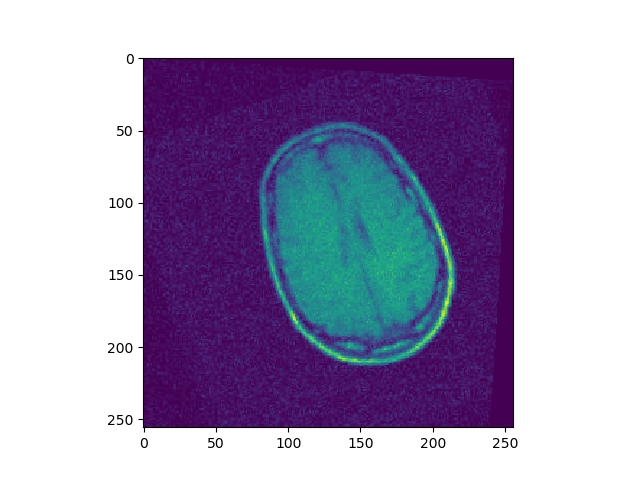
Implement a gradient descent for minimizing SSD, considering both translation and rotation. Register BrainMRI_2, 3, 4 onto BrainMRI_1.
def transform(I, theta=0, u=[0,0]):
xs, ys = np.arange(I.shape[0]), np.arange(I.shape[1])
theta = np.deg2rad(theta)
c, s = np.cos(theta), np.sin(theta)
m = np.array([[c, -s, -u[1]], [s, c, -u[0]], [0, 0 ,1]])
pts = np.array(np.meshgrid(xs, ys)).T.reshape(-1, 2)
pts = np.hstack([pts, np.ones((pts.shape[0], 1))])
out = m.dot(pts.T).T[:, :-1].reshape(I.shape[0], I.shape[1], 2)
return interpn((xs, ys), I, out, bounds_error=False, fill_value=0)
def search(I, J, lr=1e-7, iters=100):
u, t = np.zeros(2), 0
cost_history = np.zeros(iters)
x, y = np.arange(I.shape[0]), np.arange(I.shape[1])
vu, vt = np.zeros(2), 0
for itr in range(iters):
curr = transform(J, theta=t, u=u)
c, s = np.cos(np.deg2rad(t)), np.sin(np.deg2rad(t))
gy, gx = np.gradient(curr)
dx = -((curr - I) * gx).sum() * 2
dy = -((curr - I) * gy).sum() * 2
dt = -2 * ((curr - I) * (gy*(x*c-y*s) - gx*(x*s+y*c))).sum()
du = np.array([dx, dy])
cu = lr * du
ct = lr * dt
u -= cu
t -= ct
cost_history[itr] = SSD(curr, I)
return t%360, u, cost_history
t, u, ch = search(I1, I2, lr=1e-9, iters=13000)
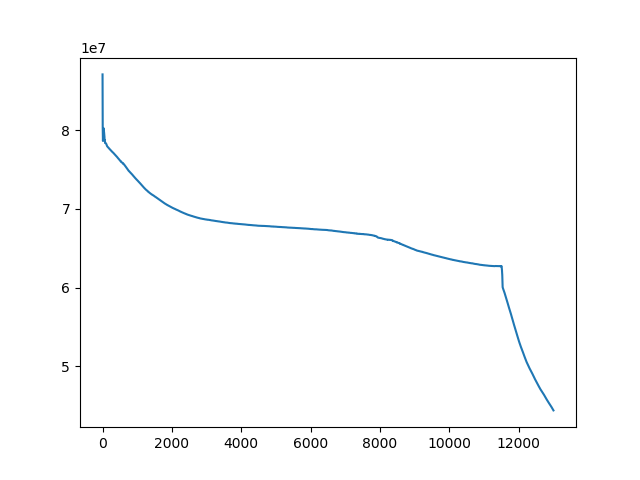
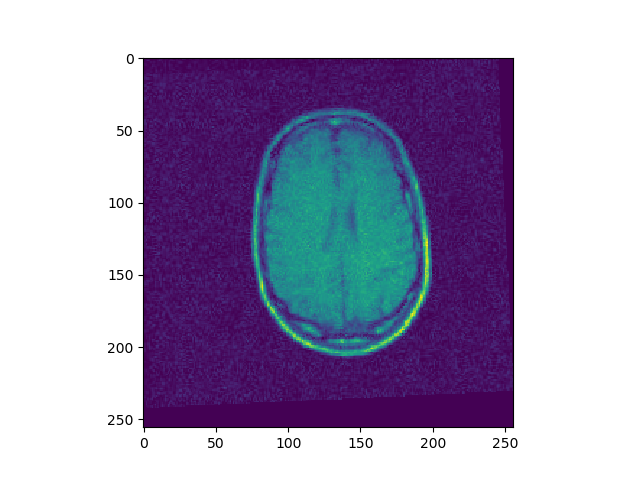
t, u, ch = search(I1, I3, lr=1e-10, iters=1000)
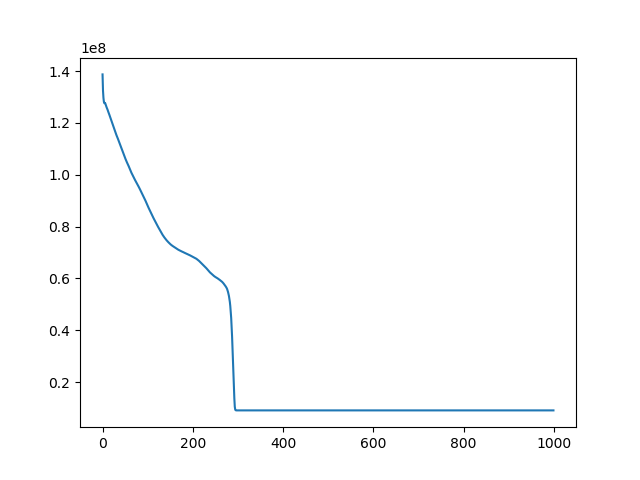
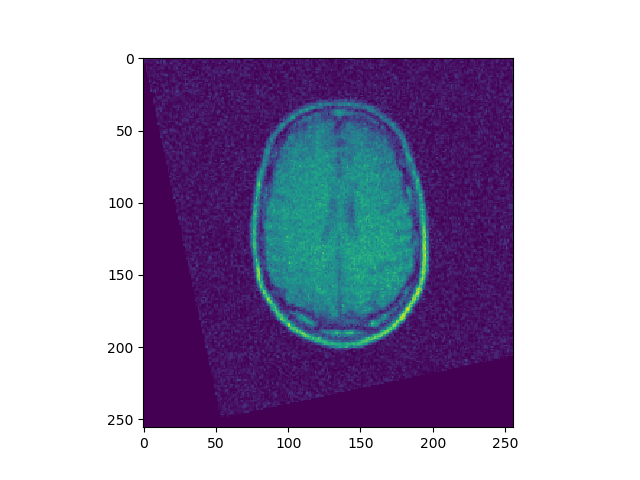
t, u, ch = search(I1, I4, lr=1e-10, iters=10000)
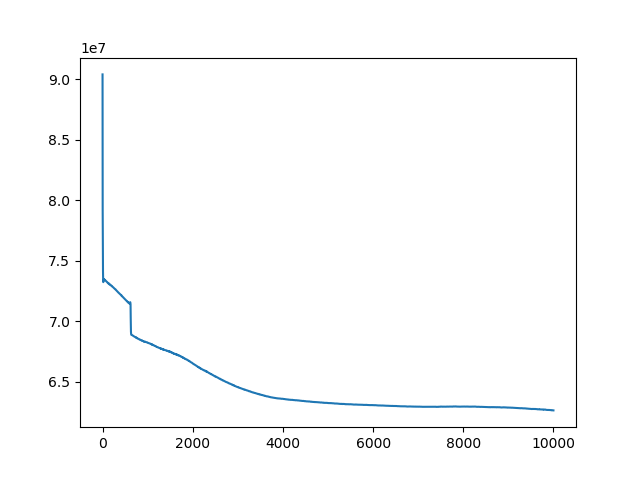
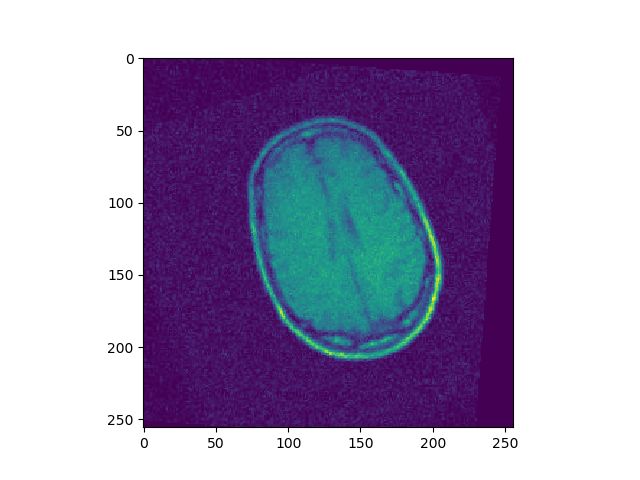
To improve the performance of gradient descent, a more advanced optimization technique is needed. Improve rigid registration with a better optimization technique. Test for the 3 cases of rigid transformations given BrainMRI_2, 3, 4.
def search(I, J, optim='gd', lr=1e-7, gamma=0.9, beta=0.9, iters=100):
u, t = np.zeros(2), 0
cost_history = np.zeros(iters)
x, y = np.arange(I.shape[0]), np.arange(I.shape[1])
vu, vt = np.zeros(2), 0
for itr in range(iters):
if optimizer == 'nag':
vu *= gamma
vt *= gamma
curr = transform(J, theta=t-vt, u=u-vu)
else:
curr = transform(J, theta=t, u=u)
c, s = np.cos(np.deg2rad(t)), np.sin(np.deg2rad(t))
gy, gx = np.gradient(curr)
dx = -((curr - I) * gx).sum() * 2
dy = -((curr - I) * gy).sum() * 2
dt = -2 * ((curr - I) * (gy*(x*c-y*s) - gx*(x*s+y*c))).sum()
du = np.array([dx, dy])
if optimizer == 'gd':
cu = lr * du
ct = lr * dt
elif optimizer == 'vgd':
cu = lr * du / I.size
ct = lr * dt / I.size
elif optimizer == 'momentum':
vu = gamma * vu + lr * du
vt = gamma * vt + lr * dt
cu, ct = vu, vt
elif optimizer == 'nag':
vu += lr * du
vt += lr * dt
cu, ct = vu, vt
elif optimizer == 'adagrad':
vu += du**2
vt += dt**2
cu = (lr / (np.sqrt(vu) + self.__eps)) * du
ct = (lr / (np.sqrt(vt) + self.__eps)) * dt
elif optimizer == 'rmsprop':
vu = beta * vu + (1-beta) * du**2
vt = beta * vt + (1-beta) * dt**2
cu = (lr / (np.sqrt(vu) + self.__eps)) * du
ct = (lr / (np.sqrt(vt) + self.__eps)) * dt
u -= cu
t -= ct
cost_history[itr] = SSD(curr, I)
return t%360, u, cost_history
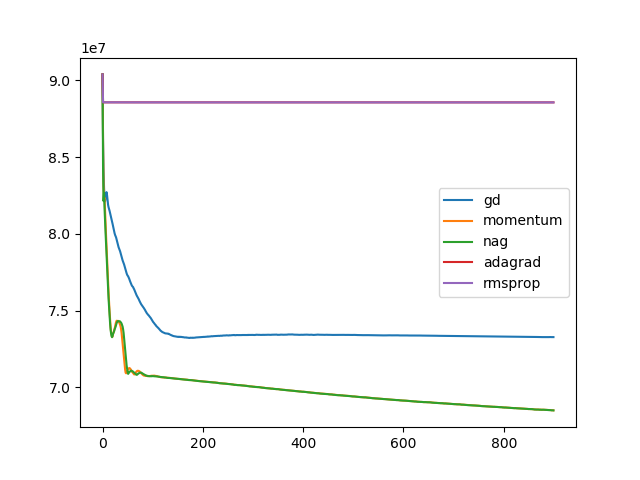
optim = ['gd', 'momentum', 'nag', 'adagrad', 'rmsprop']
for op in optim:
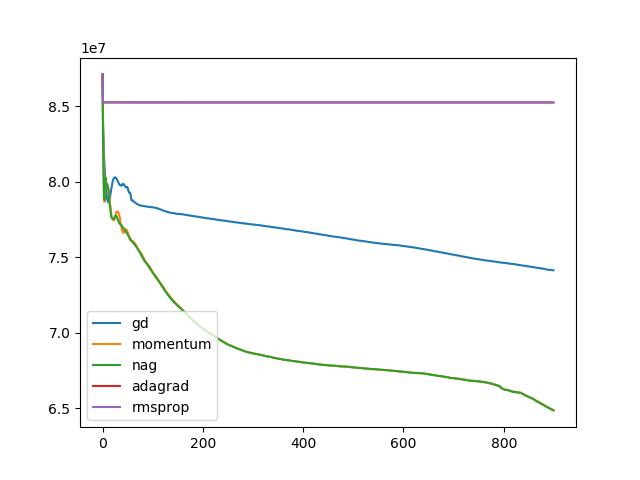
t, u, ch = search(I1, I2, optim=op, lr=1e-10, iters=900)
plt.plot(ch, label=op)
plt.legend()
for op in optim:
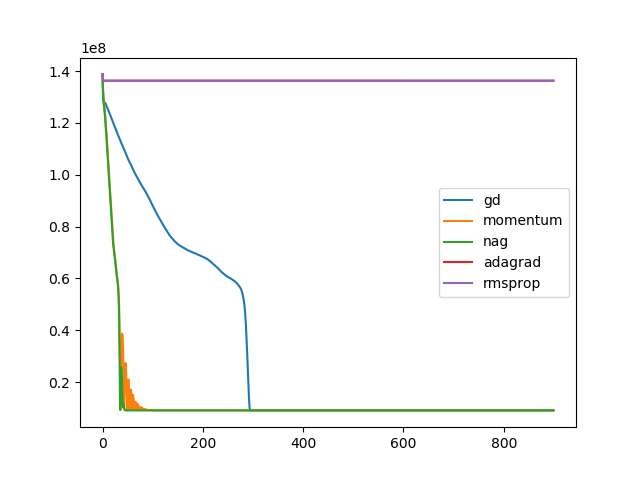
t, u, ch = search(I1, I3, optim=op, lr=1e-10, iters=900)
plt.plot(ch, label=op)
plt.legend()
for op in optim:
t, u, ch = search(I1, I4, optim=op, lr=1e-10, iters=900)
plt.plot(ch, label=op)
plt.legend()