Data Mining Basics
Objective 1
Familiarize with vector operations for manipulating multi-dimensional arrays in numpy.
- Using numpy, initialize two arrays (1000 rows, 50 and 10 columns) of random numbers each number ranging between 0 and 1;
- Create the correlation matrix (shape=[1000, 1000]) of pearson correlations between all pairs of rows from above;
- Using matplotlib, plot a 100-bin histogram, using values from lower triangle of \(1000\times1000\) correlation coefficient (r-values) matrix obtained from above (omit the diagonal and all cells above the diagonal);
- Using the histogram, estimate the probability of obtaining an r-value > 0.75 or < -0.75 from correlating two random vectors of size 50 and 10.
import numpy as np
import matplotlib.pyplot as plt
num_row = 1000
num_cols = [50, 10]
num_bins= 100
idx_low = np.tril_indices(num_row, -1)
fig, axs = plt.subplots(2, constrained_layout=True)
for idx, col in enumerate(num_cols):
arr = np.random.rand(num_row, col)
corr_mat = np.corrcoef(arr)
low_tri_arr = corr_mat[idx_low]
hist, bin_edges = np.histogram(low_tri_arr, bins=num_bins, density=True)
indices = np.logical_or(bin_edges[:-1]<-0.75, bin_edges[:-1]>0.75)
est = np.sum(hist[indices] * np.diff(bin_edges)[indices])
axs[idx].hist(low_tri_arr, bins=num_bins, density=True)
axs[idx].set_title('Probability of r-value > 0.75 or <-0.75 is {:.2f}% (size {})'.format(est*100, col))
axs[idx].set(xlabel='r-value', ylabel='probabilty')
plt.show()
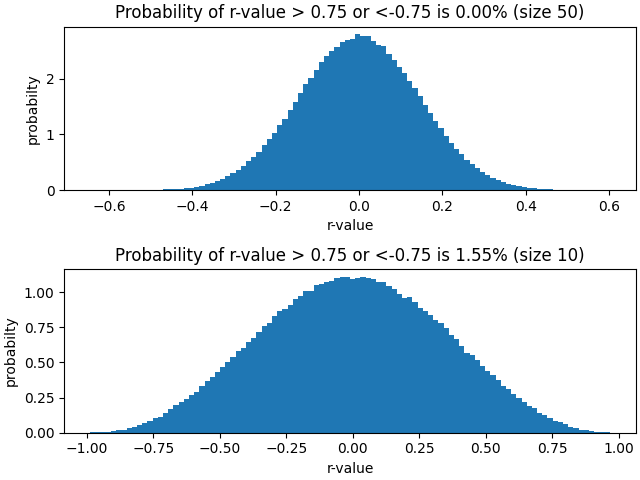
The histogram is shaped like a gaussian.
Objective 2
Basic data visualization (scatter plots and line charts).
- Get the Linnerrud dataset (import using:
from sklearn.datasets import load_linnerud). Weight, waist, and heartrate are attributes, chinups, situps, and jumps are outcomes; - Using numpy matrix functions (
np.dot,np.transpose, etc), compute the linear-least-square solution, finding the intercept and slope of best fit line for each [attribute, outcome] pair (attribute on x-axis, outcome on y-axis). Make sure to augment the attribute vectors with a column of 1’s, so LLS can find the intercept.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_linnerud
(data, target) = load_linnerud(return_X_y=True)
x_weight = target[:,0]
x_waist = target[:,1]
x_heartrate = target[:,2]
y_chinups = data[:,0]
y_situps = data[:,1]
y_jumps = data[:,2]
A_weight = np.vstack([x_weight, np.ones(len(x_weight))]).T
A_waist = np.vstack([x_waist, np.ones(len(x_waist))]).T
A_heartrate = np.vstack([x_heartrate, np.ones(len(x_heartrate))]).T
m1, c1 = np.linalg.lstsq(A_weight, data, rcond=None)[0]
m2, c2 = np.linalg.lstsq(A_waist, data, rcond=None)[0]
m3, c3 = np.linalg.lstsq(A_heartrate, data, rcond=None)[0]
fig, axs = plt.subplots(3, 3, constrained_layout=True)
axs[0, 0].plot(x_weight, y_chinups, 'o')
axs[0, 0].plot(x_weight, m1[0]*x_weight + c1[0])
axs[0, 0].set_title('Slope: {:.2f}\nIntercept: {:.2f}'.format(m1[0], c1[0]))
axs[0, 0].set(xlabel='weight', ylabel='chinups')
axs[0, 1].plot(x_weight, y_situps, 'o')
axs[0, 1].plot(x_weight, m1[1]*x_weight + c1[1])
axs[0, 1].set_title('Slope: {:.2f}\nIntercept: {:.2f}'.format(m1[1], c1[1]))
axs[0, 1].set(xlabel='weight', ylabel='situps')
axs[0, 2].plot(x_weight, y_jumps, 'o')
axs[0, 2].plot(x_weight, m1[2]*x_weight + c1[2])
axs[0, 2].set_title('Slope: {:.2f}\nIntercept: {:.2f}'.format(m1[2], c1[2]))
axs[0, 2].set(xlabel='weight', ylabel='jumps')
axs[1, 0].plot(x_waist, y_chinups, 'o')
axs[1, 0].plot(x_waist, m2[0]*x_waist + c2[0])
axs[1, 0].set_title('Slope: {:.2f}\nIntercept: {:.2f}'.format(m2[0], c2[0]))
axs[1, 0].set(xlabel='waist', ylabel='chinups')
axs[1, 1].plot(x_waist, y_situps, 'o')
axs[1, 1].plot(x_waist, m2[1]*x_waist + c2[1])
axs[1, 1].set_title('Slope: {:.2f}\nIntercept: {:.2f}'.format(m2[1], c2[1]))
axs[1, 1].set(xlabel='waist', ylabel='situps')
axs[1, 2].plot(x_waist, y_jumps, 'o')
axs[1, 2].plot(x_waist, m2[1]*x_waist + c2[1])
axs[1, 2].set_title('Slope: {:.2f}\nIntercept{:.2f}'.format(m2[2], c2[2]))
axs[1, 2].set(xlabel='waist', ylabel='jumps')
axs[2, 0].plot(x_heartrate, y_chinups, 'o')
axs[2, 0].plot(x_heartrate, m3[0]*x_heartrate + c3[0])
axs[2, 0].set_title('Slope: {:.2f}\nIntercept: {:.2f}'.format(m3[0], c3[0]))
axs[2, 0].set(xlabel='heartrate', ylabel='chinups')
axs[2, 1].plot(x_heartrate, y_situps, 'o')
axs[2, 1].plot(x_heartrate, m3[1]*x_heartrate + c3[1])
axs[2, 1].set_title('Slope: {:.2f}\nIntercept: {:.2f}'.format(m3[1], c3[1]))
axs[2, 1].set(xlabel='heartrate', ylabel='situps')
axs[2, 2].plot(x_heartrate, y_jumps, 'o')
axs[2, 2].plot(x_heartrate, m3[2]*x_heartrate + c3[2])
axs[2, 2].set_title('Slope: {:.2f}\nIntercept: {:.2f}'.format(m3[2], c3[2]))
axs[2, 2].set(xlabel='heartrate', ylabel='jumps')
plt.show()

Objective 3
To understand the basic machine learning algorithms, here I implement the following two algorithms, from scratch, in python (using only numpy import). And test these algorithms on the Linnerrud dataset (import using: from sklearn.datasets import load_linnerud) using all 3 attributes, and only the chinups outcome. Define new vector assigning binary classes to the outcome of chinups as follows:
if (chinups > median(chinups)) then chinups = 0 else chinups = 1
import numpy as np
from sklearn.datasets import load_linnerud
(data, target) = load_linnerud(return_X_y=True)
chinups = data[:,0]
median = np.median(chinups)
chinups = np.where(chinups > median, 1, 0)
then use these classes to build the probability table and train the perceptron.
Gaussian Naive Bayes
Gaussian Naive Bayes is a probabilistic modeling algorithm.
- Gaussian Naive Bayes (probabilistic modeling)
class GNB():
def __init__(self):
self._mu0 = []
self._mu1 = []
self._sigma0 = []
self._sigma1 = []
self._prior = {}
def _prior_prob(self, y):
unique, counts = np.unique(y, return_counts=True)
prob = counts/len(y)
return dict(zip(unique, prob))
def fit(self, X, y):
self._mu0 = np.mean(X[y==0], axis=0)
self._mu1 = np.mean(X[y==1], axis=0)
self._sigma0 = np.std(X[y==0], axis=0)
self._sigma1 = np.std(X[y==1], axis=0)
self._prior = self._prior_prob(y)
def pred(self, x):
x0 = x
x1 = x
probs0 = np.ones(x.shape)
probs1 = np.ones(x.shape)
for i in range(x.shape[1]):
gaussian0 = lambda x: 1/(np.sqrt(2*np.pi)*self._sigma0[i])*np.exp((-(x-self._mu0[i])**2)/(2*self._sigma0[i]**2))
gaussian1 = lambda x: 1/(np.sqrt(2*np.pi)*self._sigma1[i])*np.exp((-(x-self._mu1[i])**2)/(2*self._sigma1[i]**2))
v_gaussian0 = np.vectorize(gaussian0)
v_gaussian1 = np.vectorize(gaussian1)
probs0[:,i] = v_gaussian0(x0[:,i])
probs1[:,i] = v_gaussian1(x1[:,i])
likeli0 = np.prod(probs0, axis=1)*self._prior[0]
likeli1 = np.prod(probs1, axis=1)*self._prior[1]
post = likeli1 / (likeli0+likeli1)
return post
gnb = GNB()
gnb.fit(target, chinups)
outputs = gnb.pred(target)
print(((outputs > 0.5) == chinups).sum() / len(chinups))
0.7
Perceptron
Perceptron learning rule is linear modeling algorithm.
class Perceptron(object):
# if perceptron does not converge run for 1000 iterations
def __init__(self, iters=1000):
self._iters = iters
self._weights = []
def fit(self, X, y):
# set all weights to zero
self._weights = np.zeros(X.shape[1]+1)
# until all instances in training set are correctly classified
# or run enough iterations
for _ in range(self._iters):
y_pred = self.pred(X)
y_pred = y_pred>0
if np.all(y_pred==y):
break
for inst, label in zip(X, y): # for each instance
pred = self._pred(inst)
if pred != label: # if inst is classed incorrectly
# if inst belongs to first class, add to weight vec
# else subtract it from weight vec
self._weights[1:] += (label - pred) * inst
self._weights[0] += (label - pred)
def _pred(self, inst):
prediction = np.dot(inst, self._weights[1:]) + self._weights[0]
if prediction > 0:
prediction_class = 1
else:
prediction_class = 0
return prediction_class
def pred(self, x):
weighted_sums = np.dot(x, self._weights[1:]) + self._weights[0]
return weighted_sums
perceptron = Perceptron()
perceptron.fit(target, chinups)
outputs = perceptron.pred(target)
print(((outputs > 0) == chinups).sum() / len(chinups))
0.5