Validation Techniques in scikit-learn
Goal
Here just test a variety of classifiers on different datasets in sklearn, and test validation techniques (cross-validation, ROC, t-test). It mainly just involves calling sklearn functions and displaying results.
Classification and Regression
Classifiers
Import and load the toy datasets from sklearn:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston, load_iris, load_diabetes, load_digits, load_linnerud, load_wine, load_breast_cancer
boston = load_boston() # regression
iris = load_iris() # classification
diabetes = load_diabetes() # regression
digits = load_digits() # classification
linnerud = load_linnerud() # regression
wine = load_wine() # classification
cancer = load_breast_cancer() # classification
Import and initialize the following classifers from sklearn:
from sklearn.naive_bayes import GaussianNB
from sklearn import tree
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neural_network import MLPClassifier
gnb = GaussianNB() # probabilistic
tree = tree.DecisionTreeClassifier() # divide and conquer
knn = KNeighborsClassifier(3, n_jobs=-1) # instance based
mlp = MLPClassifier() # neural network
Train and run each classifier on each classification dataset separately, resulting in a 4x4 matrix (dataset rows, classifier columns) showing the accuracy of 4 classifiers above on each classification dataset (here use entire dataset, no test/train split). Classification datasets are iris, digits, wine, breast cancer. Display this matrix using imshow from matplotlib. Using the 4x4 matrix, we can get classifier which has highest mean accuracy across all datasets and dataset which has the highest mean accuracy across all classifiers:
clfs = [gnb, tree, knn, mlp]
clf_data = [iris, digits, wine, cancer]
clf_mat = np.zeros((len(clf_data), len(clfs)))
for i in range(len(clf_data)):
for j in range(len(clfs)):
clf_mat[i,j] = clfs[j].fit(clf_data[i].data, clf_data[i].target).score(clf_data[i].data, clf_data[i].target)
datasets = ['iris', 'digits', 'wine', 'cancer']
classifiers = ['GaussianNB', 'DecisionTree', 'KNN', 'MLP']
max_clf = classifiers[np.argmax(np.mean(clf_mat, axis=0))]
max_clf_dataset = datasets[np.argmax(np.mean(clf_mat, axis=1))]
plt.imshow(clf_mat, cmap='viridis')
plt.yticks(range(4), datasets)
plt.xticks(range(4), classifiers)
plt.xlim([-0.5, 3.5])
plt.colorbar()
plt.title('top classifier='+max_clf +', top dataset='+ max_clf_dataset)
plt.show()

Regressors
Import and initialize the following regression algorithms from sklearn:
from sklearn import linear_model
from sklearn import svm
reg = linear_model.LinearRegression(n_jobs=-1) # linear regression
svr = svm.SVR(gamma='scale') # support vector regression
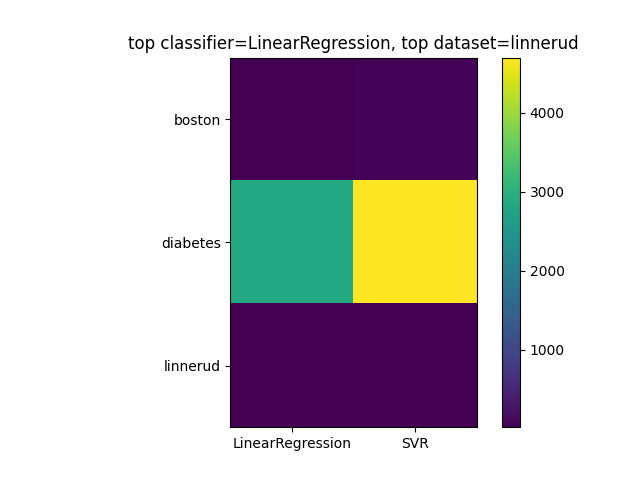
Create a 3x2 matrix (dataset rows, classifier columns) showing accuracy of 2 regression techniques above on the three regression datasets (for linnerud, use only chinups). Get regression technique which has lower mean-squared error (across datasets) and dataset which has lowest mean squared-error (across regression methods):
# can't use loop because of irregular formats (linnerud)
from sklearn.metrics import mean_squared_error
regs = [reg, svr]
regsets = [boston, diabetes, linnerud]
regmat = np.zeros((len(regsets), len(regs)))
# fit boston with linear regression
reg = regs[0].fit(regsets[0].data,regsets[0].target)
regmat[0,0] = mean_squared_error(reg.predict(regsets[0].data),regsets[0].target)
# fit boston with svr
reg = regs[1].fit(regsets[0].data,regsets[0].target)
regmat[0,1] = mean_squared_error(reg.predict(regsets[0].data),regsets[0].target)
# fit diabetes with linear regression
reg = regs[0].fit(regsets[1].data,regsets[1].target)
regmat[1,0] = mean_squared_error(reg.predict(regsets[1].data),regsets[1].target)
# fit diabetes with svr
reg = regs[1].fit(regsets[1].data,regsets[1].target)
regmat[1,1] = mean_squared_error(reg.predict(regsets[1].data),regsets[1].target)
# fit chinups of linnerud with linear regression
reg = regs[0].fit(regsets[2].target,regsets[2].data[:,0])
regmat[2,0] = mean_squared_error(reg.predict(regsets[2].target),regsets[2].data[:,0])
# fit chinups of linnerud with support vector regression
reg = regs[1].fit(regsets[2].target,regsets[2].data[:,0])
regmat[2,1] = mean_squared_error(reg.predict(regsets[2].target),regsets[2].data[:,0])
datasets = ['boston', 'diabetes', 'linnerud']
regs = ['LinearRegression', 'SVR']
max_reg = regs[np.argmin(np.mean(regmat, axis=0))]
max_reg_dataset = datasets[np.argmin(np.mean(regmat, axis=1))]
plt.imshow(regmat, cmap='viridis')
plt.yticks(range(3), datasets)
plt.xticks(range(2), regs)
plt.xlim([-0.5, 1.5])
plt.colorbar()
plt.title('top classifier='+max_reg +', top dataset='+ max_reg_dataset)
plt.show()
California housing predictions and validation
Fetch California housing dataset:
from sklearn.datasets import fetch_california_housing
cali = fetch_california_housing()
- Using Gaussian Naive Bayes, for each instance output a probability that the house is worth over \(\$300\)k (target variable is in units of \(\$100,000\)’s):
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(cali.data, cali.target>3)
probs = gnb.predict_proba(cali.data)[:,1]
- Perform k-fold (k=10) cross-validation (CV) and find the average error across all folds on the test set (using GNB) and the resubstitution error (error on training data):
from sklearn.model_selection import cross_val_score
scores = cross_val_score(gnb, cali.data, cali.target>3, cv=10)
print('Average error:', 1-np.mean(scores))
print('Resubstitution error:', 1-(np.mean(gnb.score(cali.data, cali.target>3))))
Average error: 0.16167635658914725
Resubstitution error: 0.13187984496124028
- Plot the ROC curve using the training data above, this is also known as the ‘resubstitution ROC area’ (ROC from training data), i.e., train GNB on all the instances, then calculate ROC area using probabilities from predictions on instances that GNB was trained on. Also try to increase the area under ROC by denoising or removing attributes, of performing some other type of transformation (PCA, PLS, etc.):
from sklearn import metrics
def roc_auc(clf,data,target):
clf.fit(data,target)
fpr, tpr, thresholds = metrics.roc_curve(target,clf.predict_proba(data)[:,1])
return metrics.auc(fpr,tpr)
aucs = []
clf = GaussianNB();
aucs.append(roc_auc(clf,cali.data,cali.target>3))
from sklearn.decomposition import MiniBatchDictionaryLearning, FactorAnalysis, FastICA, PCA
n_comps = 8
denoise_types = ['no denoising','dictionary','fastica','factor','pca','pls','cca','plsr','plssvd']
dlearn_data = MiniBatchDictionaryLearning(n_components=n_comps).fit_transform(cali.data)
aucs.append(roc_auc(clf,dlearn_data,cali.target>3))
fastica_data = FastICA(n_components=n_comps).fit_transform(cali.data)
aucs.append(roc_auc(clf,fastica_data,cali.target>3))
factored_data = FactorAnalysis(n_components=n_comps).fit_transform(cali.data)
aucs.append(roc_auc(clf,factored_data,cali.target>3))
pca_data = PCA(n_components=n_comps).fit_transform(cali.data)
aucs.append(roc_auc(clf,pca_data,cali.target>3))
from sklearn.cross_decomposition import PLSCanonical, PLSRegression, CCA, PLSSVD
pls_data = PLSCanonical(n_components=n_comps).fit_transform(cali.data,cali.target)[0]
aucs.append(roc_auc(clf,pls_data,cali.target>3))
cca_data = CCA(n_components=n_comps).fit_transform(cali.data,cali.target)[0]
aucs.append(roc_auc(clf,cca_data,cali.target>3))
plsr_data = PLSRegression(n_components=n_comps).fit_transform(cali.data,cali.target)[0]
aucs.append(roc_auc(clf,plsr_data,cali.target>3))
plssvd_data = PLSSVD(n_components=n_comps).fit_transform(cali.data,cali.target)[0]
aucs.append(roc_auc(clf,plssvd_data,cali.target>3))
plt.legend([m+': '+str(n) for m,n in zip(denoise_types,aucs)])
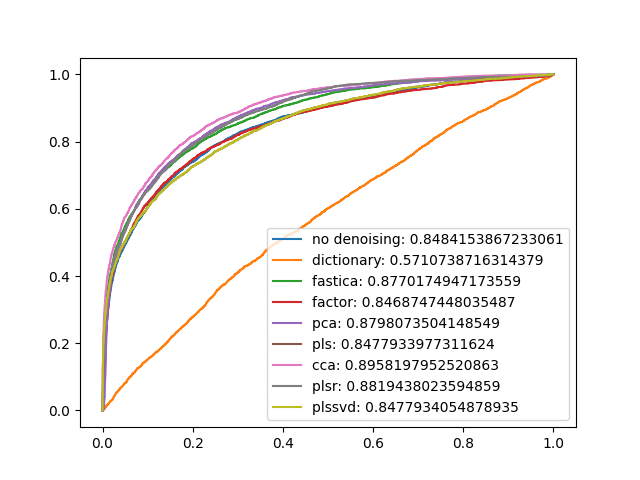
It seems canonical correlation analysis is most useful (on this dataset).
Using the following 3 classifiers:
- Gaussian Naive Bayes (same as above)
- k-nearest neighbour with k=3 (it can output probabilities)
- random forest (also outputs probabilities)
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(n_estimators=100, n_jobs=-1)
kneigh = KNeighborsClassifier(n_neighbors=3, n_jobs=-1)
gnb = GaussianNB()
- Plot the average ROC curve with error bars over 10 tests sets from 10-fold CV, (i.e., calculate one ROC area for each fold’s test set predictions, and average them all to create a single ROC area):
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import roc_curve, auc
tprs = np.zeros([3,10,100])
aucs = np.zeros([3,10])
mean_fpr = np.linspace(0, 1, 100)
cv = StratifiedKFold(n_splits=10)
X = cali.data
y = cali.target > 3
i = 0
clfcount=0
for clf in [forest,kneigh,gnb]:
for train, test in cv.split(X, y):
probas_ = clf.fit(X[train], y[train]).predict_proba(X[test])
fpr, tpr, thresholds = roc_curve(y[test], probas_[:, 1])
tprs[clfcount,i,:] = np.interp(mean_fpr, fpr, tpr)
roc_auc = auc(fpr, tpr)
aucs[clfcount,i] = roc_auc
i += 1
clfcount += 1
i=0
for i in np.arange(0,3):
plt.errorbar(np.arange(0,100),np.mean(tprs[i,:,:],axis=0),\
np.std(tprs[i,:,:],axis=0))
clf_types = ['forest','kneigh','gnb']
plt.legend([m+': '+str(n) for m,n in zip(clf_types,np.mean(aucs,axis=1))])
plt.show()
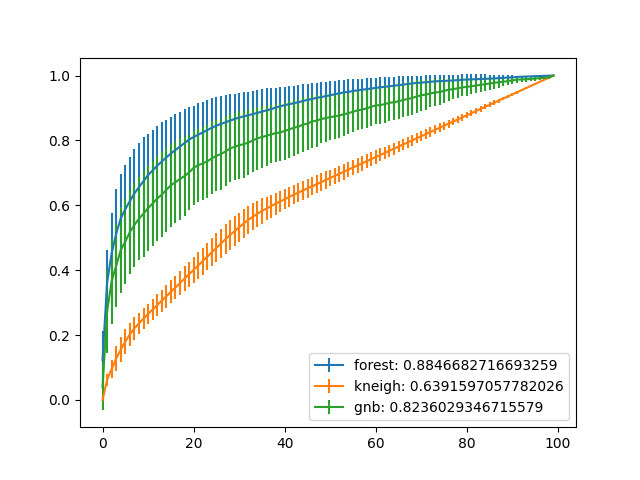
Random Forest algorithm gives the highest area under average ROC curve from results.
- Using a t-test, compare the algorithm with the highest performance to the other two algorithms, and check if the p-value is significant (p<0.05):
from scipy import stats
t_1,p_1 = stats.ttest_ind(aucs[0,:],aucs[1,:])
t_2,p_2 = stats.ttest_ind(aucs[0,:],aucs[2,:])
print('P-value (RF vs GNB): {} < 0.05 => {}'.format(p_2, p_2<0.05))
print('P-value (RF vs KNN): {} < 0.05 => {}'.format(p_1, p_1<0.05))
P-value (RF vs GNB): 0.041641516493412564 < 0.05 => True
P-value (RF vs KNN): 9.452363626206385e-11 < 0.05 => True