MRI Image Viewer
All these images were taken from OpenNeuro. Use the nibabel libraries to load images from disk. Here we use Python and Numpy libraries. There 5 separate modalities of 3D MRI images as follows:
- T1-weighted (t1.nii)
- T2-weighted (t2.nii)
- Susceptibility-weighted (swi.nii)
- Time of flight angiogram (tof.nii)
- Blood oxygen level dependent (bold.nii)
.nii is a medical imaging format (nifti format).
Python viewer
Create a viewer function in Python that displays a slice from a 3D image and allows for scrolling through the images slices using keypad or mouse wheel. A call to viewer(t1_data, index=250, view='coronal') produce the following image:
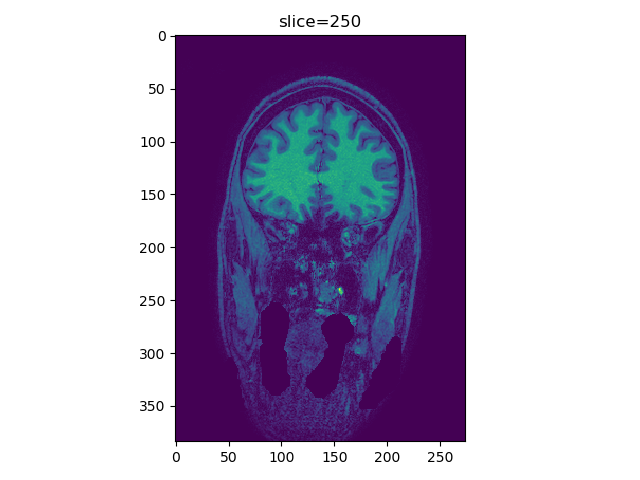
t1_data is a 3D numpy array with the z-slices in the \(3^\text{rd}\) dimension (most images are structured this way). We can rotate the mouse wheel, or press the ‘up’ or ‘down’ arrow keys, the image will change to a different slice. Here uses of the Matplotlib.
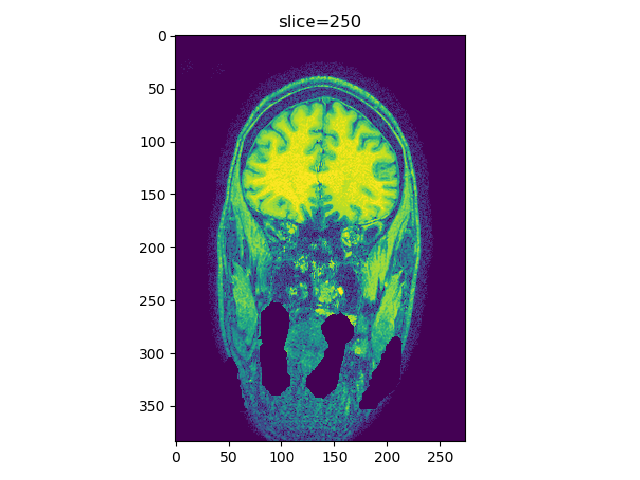
Add histogram equalization option histeq, call viewer(t1_data, index=250, view='coronal', histeq=True) will produce a histogram-equalized image in the viewer, instead of the raw image.
Add an option to display all viewers simultaneously in the same plot using sub-plots. When place the mouse over one of the subplots and rotate the mouse wheel, only the selected subplot slice will change. viewer(t1_data, index=250, view='all'):
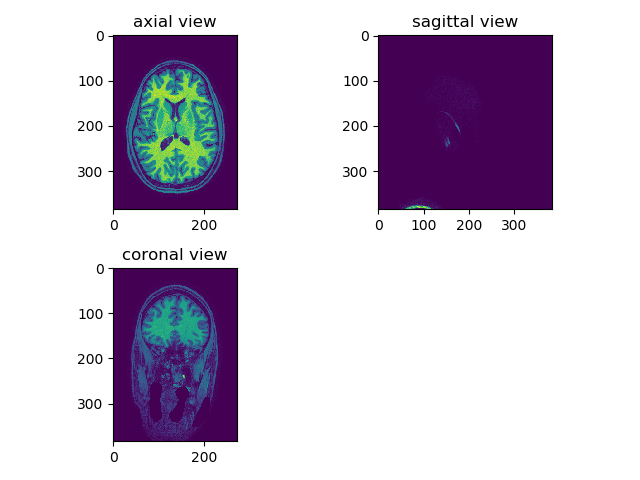
We can also see the need for histogram equalization in sagittal/coronal view (blood vessels are too bright relative to the rest of the tissue). Also add different colormaps and intensity limits options, viewer(t1_data, index=250, view='axial', cmap='gray'):
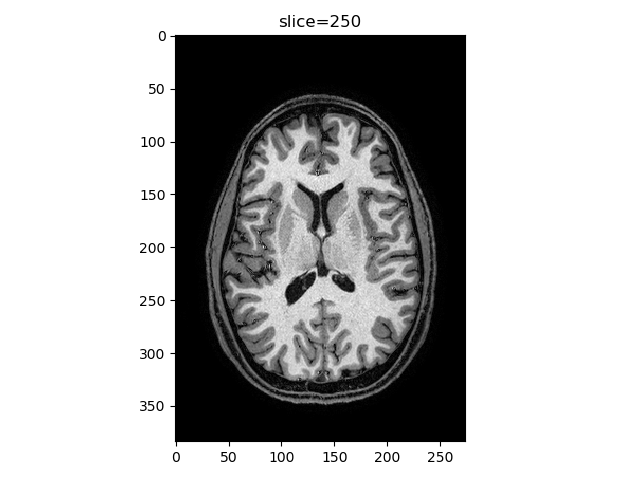
viewer(t1_data, index=250, view='axial', cmap='jet')
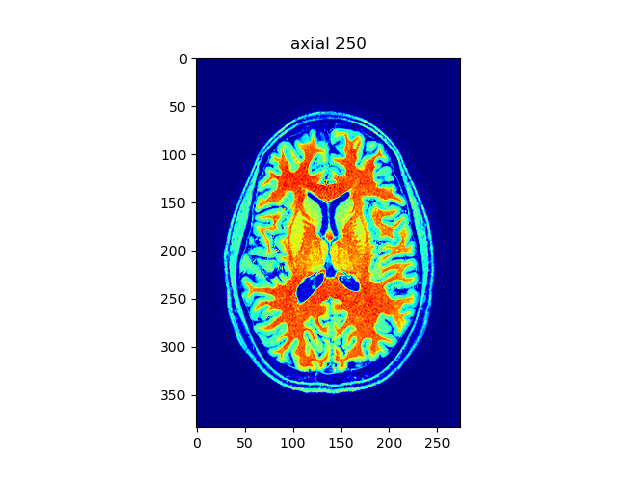
viewer(t1_data, index=250, view='axial', cmap='hot')
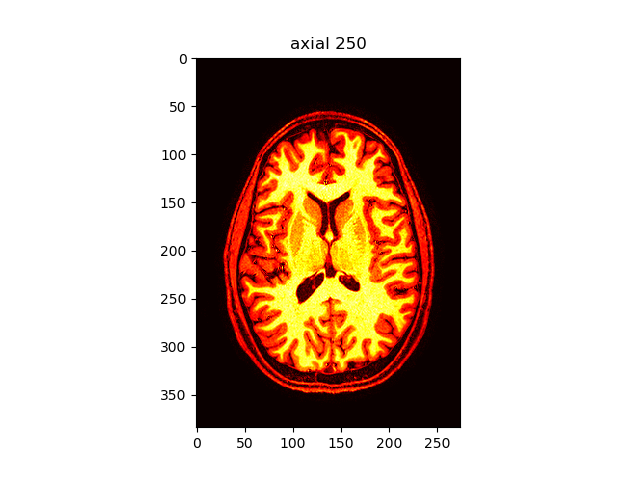
viewer(t1_data, index=250, view='axial', vmin=20, vmax=60)
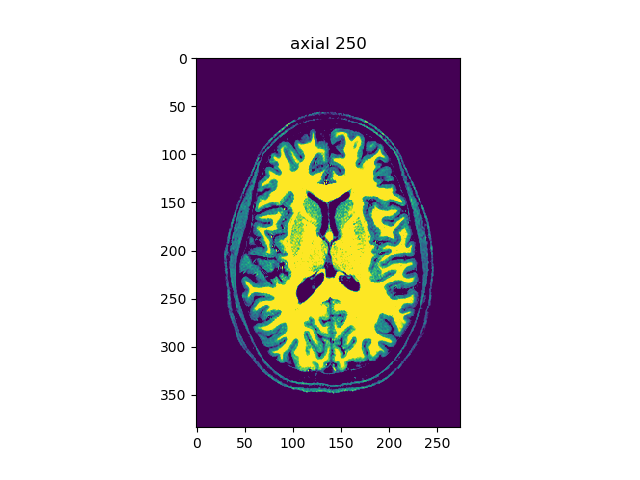
viewer(t1_data, index=250, view='axial', aspect='auto')
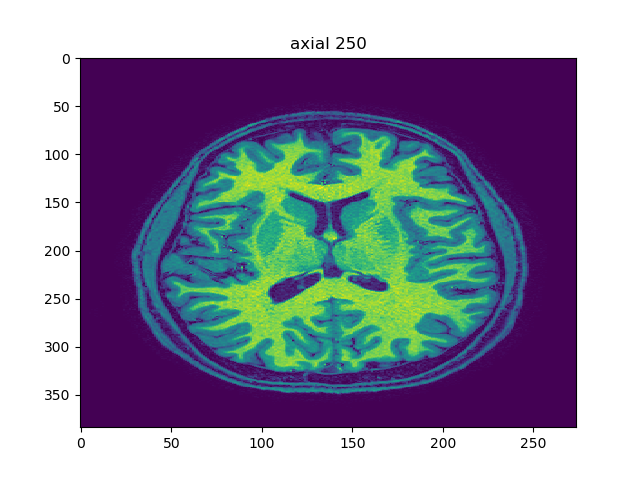
Modalities and frequency-domain filtering
Smoothing and edge-detection are fundamental image processing operations. Here we use fft functions in numpy to perform edge detection and smoothing on 3D images in the frequency domain. Do a simple 2D FFT on one of the z-slices (axial slice) and display the result. Here uses fftshift and the logarithm to correctly visualize the fft. It looks like below using t2.nii, viewer(t2_data, index=250, view='axial'):
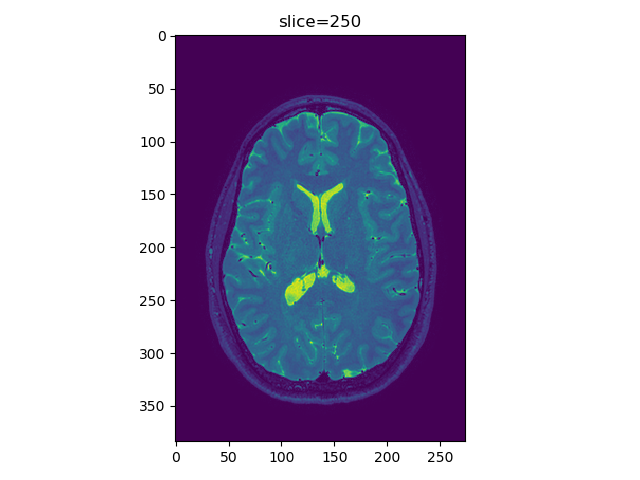
viewer(t2_data, index=250, view='axial', fft=True)
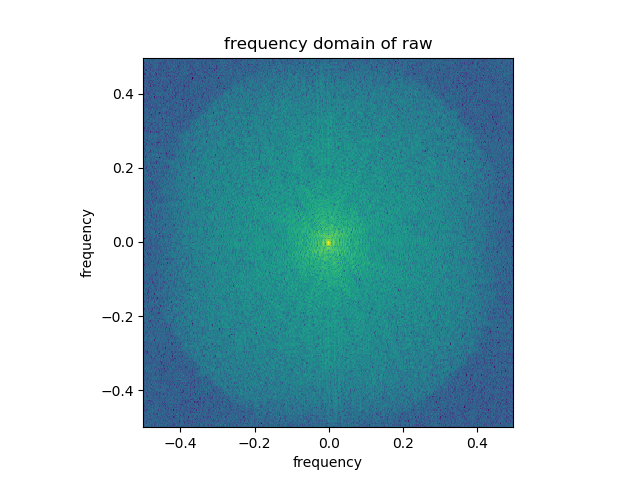
Generate frequency-domain gaussian filter using meshgrid and use to do frequency space filtering. Generating filters for 5 different sigmas using the following code:
# Gaussian filter
def gaussian_kernel(size, sigma=10, ptype='low', dim=2, verbose=False):
if dim == 1:
norm_v = np.vectorize(lambda x: np.exp(-(x/sigma)**2 / 2) /\
(np.sqrt(2*np.pi)*sigma))
kernel = norm_v(np.linspace(-size // 2, size // 2, size))
elif dim == 2:
sz_x, sz_y = size
X, Y = np.mgrid[:sz_x, :sz_y]
xpr = X - int(sz_x) // 2
ypr = Y - int(sz_y) // 2
kernel = np.exp(-((xpr**2+ypr**2) / (2*sigma**2))) / (2*np.pi*sigma**2)
if ptype == 'high':
kernel = 1 - kernel
if verbose:
plt.title('sigma=%d' % sigma)
if dim == 1:
plt.plot(kernel)
elif dim == 2:
plt.imshow(kernel)
return kernel
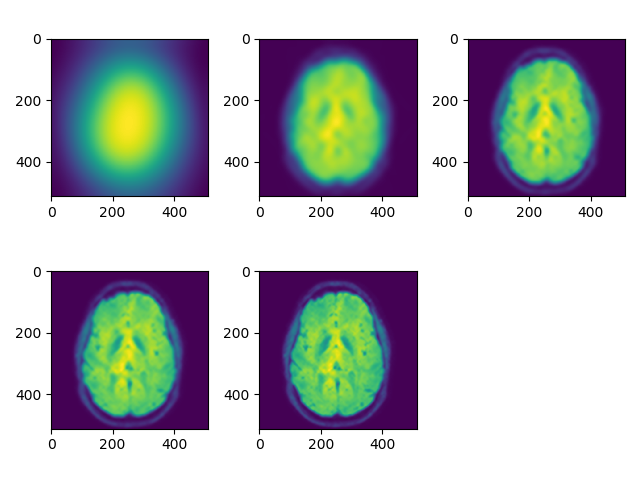
Below is the corresponding image after multiplying the above filter with the Fourier transform of raw and then inverting the Fourier transform on the swi.nii imaging modality:
# load swi
swi_data = nib.load('images/swi.nii').get_fdata()
# Gaussian blur
rotim = viewer(swi_data, index=250, view='axial', fft=True, ret_val=True)
count = 1
for sigma in range(1, 25, 5):
gaussfilt = gaussian_kernel(rotim.shape, sigma=sigma)
plt.subplot(2, 3, count)
plt.imshow(np.abs(np.fft.ifft2(np.fft.ifftshift(gaussfilt*rotim))))
count += 1
plt.suptitle('Gaussian blur')
plt.tight_layout()
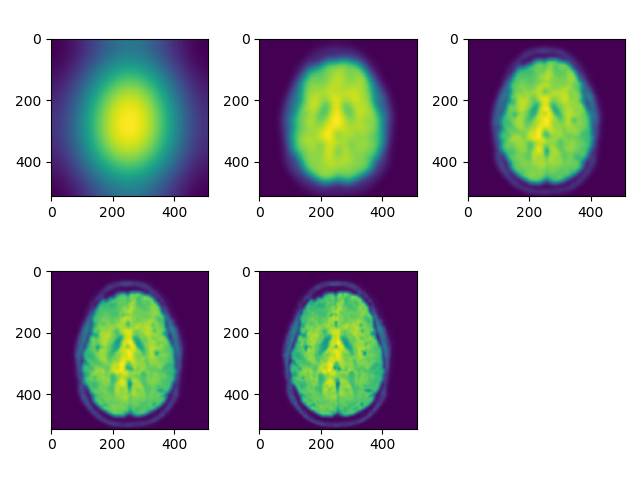
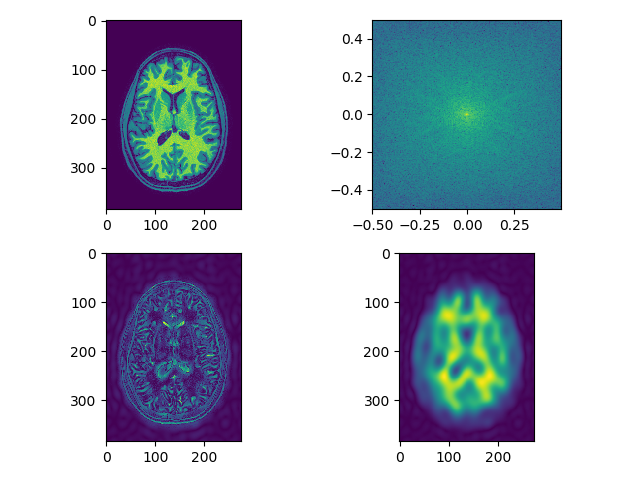
Load and display each modality in viewer. Perform smoothing as above and also edge detection using frequency domain filtering on each modality, can use fftn, or just do a 2D version and show a single slice. Let’s show the result as 5 separate plots (1 for each modality), each plot has 4 sub-plots:
- raw image (single slice)
- fft (raw image) – shown as above
- raw image after edge enhancement using frequency domain filtering (edge detection filter)
- raw image after smoothing using frequency domain filtering (use filters defined as above)
# Circular pass filter mask
def cpf(size, r=10, ptype='high', verbose=False):
rows, cols = size
crow, ccol = int(rows / 2), int(cols / 2)
cntr = [crow, ccol]
x, y = np.ogrid[:rows, :cols]
if ptype == 'band':
mask_area = np.logical_and(((x-cntr[0])**2 + (y-cntr[1])**2 >= r[0]**2),
((x-cntr[0])**2 + (y-cntr[1])**2 <= r[1]**2))
else:
mask_area = (x - cntr[0]) ** 2 + (y - cntr[1]) ** 2 <= r**2
if ptype == 'high':
mask = np.ones((rows, cols))
mask[mask_area] = 0
elif ptype == 'low' or ptype == 'band':
mask = np.zeros((rows, cols))
mask[mask_area] = 1
if verbose:
plt.imshow(mask)
plt.title("Pass filter")
return mask
def separate_axial(data, index=250):
# raw image
plt.subplot(221)
plt.imshow(np.rot90(data[:, :, index]))
# fft
plt.subplot(222)
rotim = np.fft.fftshift(np.rot90(np.fft.fftn(data, axes=(0,1))[:, :, index]))
freq_x = np.fft.fftfreq(rotim.shape[0])
freq_y = np.fft.fftfreq(rotim.shape[1])
plt.imshow(np.abs(np.log(rotim)), extent=(freq_x.min(), freq_x.max(),
freq_y.min(), freq_y.max()))
# edge enhancement
plt.subplot(223)
hpf = cpf(rotim.shape, ptype='high')
plt.imshow(np.abs(np.fft.ifft2(np.fft.ifftshift(hpf*rotim))))
# smoothing
plt.subplot(224)
lpf = cpf(rotim.shape, ptype='low')
plt.imshow(np.abs(np.fft.ifft2(np.fft.ifftshift(lpf*rotim))))
plt.suptitle('axial %d' % index)
plt.tight_layout()
# separate plot t1
separate_axial(t1_data, index=250)
# separate plot t2
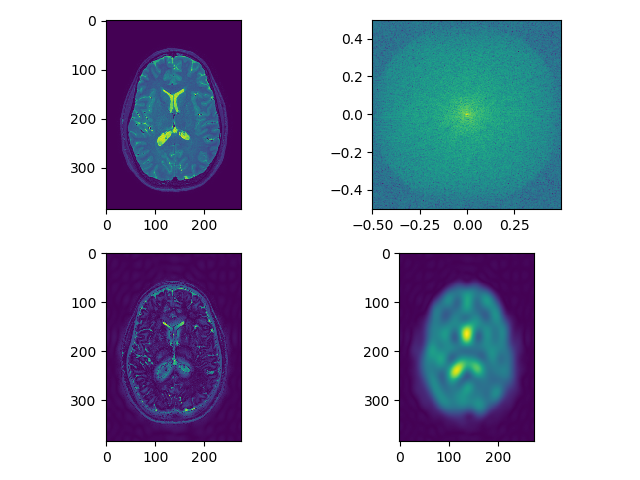
separate_axial(t2_data, index=250)
# separate plot swi
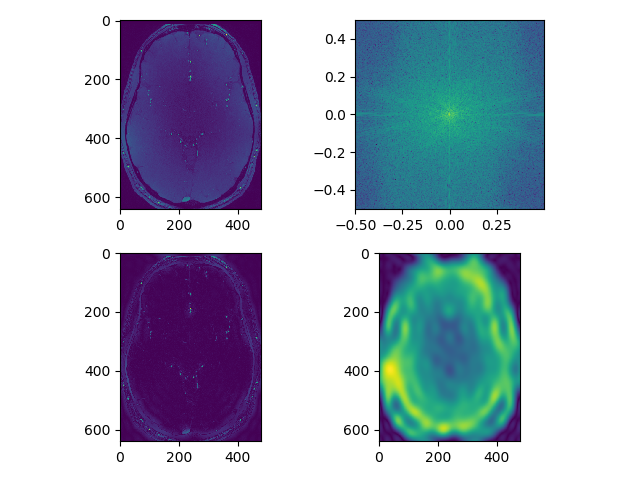
separate_axial(swi_data, index=250)
# load tof
tof_data = nib.load('images/tof.nii').get_fdata()
# separater plot tof
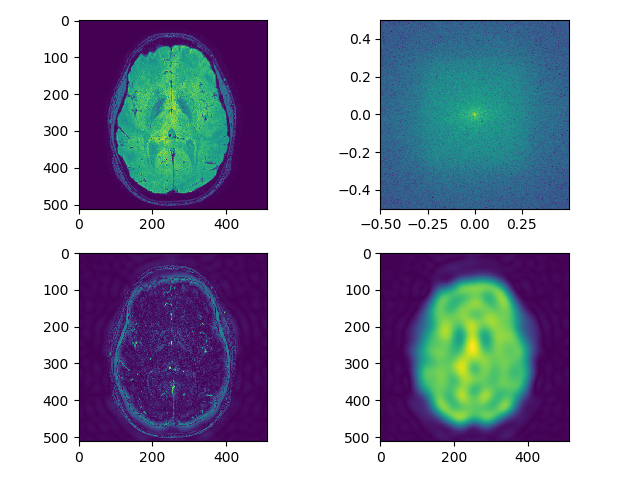
separate_axial(tof_data, index=50)
# load bold
bold_data = nib.load('images/bold.nii').get_fdata()
# separate plot bold
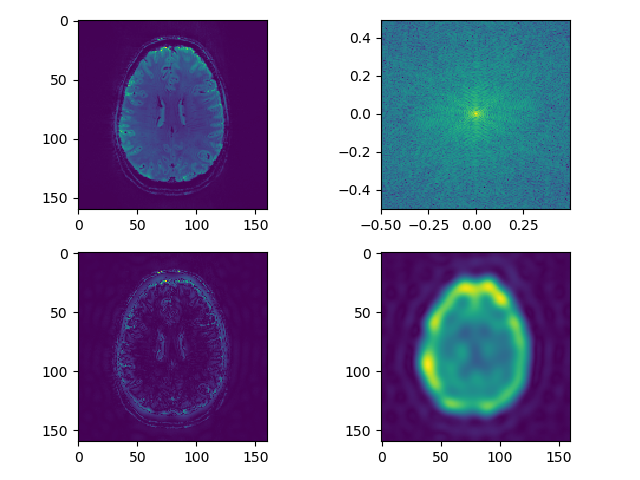
separate_axial(bold_data, index=30)
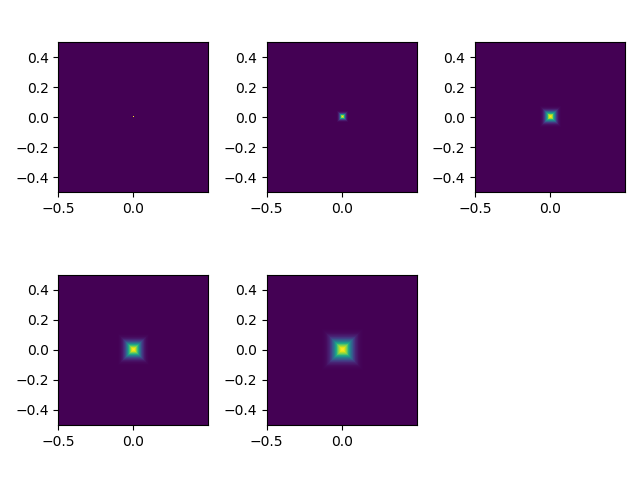
Now experiment with different filter shape. Use a bar or a square, instead of a Gaussian smooth. Use square filter to multiply fourier transform of the image:
def square_kernel(size, a=21, ptype='low', verbose=False):
rows, cols = size
xline = np.ones(rows)
yline = np.ones(cols)
xf = gaussian_kernel(rows, sigma=a, dim=1, ptype=ptype)
yf = gaussian_kernel(cols, sigma=a, dim=1, ptype=ptype)
xkernel = np.outer(xline.T, yf.T)
ykernel = np.outer(xf.T, yline.T)
kernel = np.minimum(xkernel, ykernel)
if verbose:
plt.imshow(kernel)
plt.title("Square filter")
return kernel
rotim = viewer(swi_data, index=250, view='axial', fft=True, ret_val=True)
freq_x = np.fft.fftfreq(rotim.shape[0])
freq_y = np.fft.fftfreq(rotim.shape[1])
count = 1
for a in range(1, 25, 5):
plt.subplot(2, 3, count)
plt.imshow(square_kernel(rotim.shape, a=a),
extent=(freq_x.min(), freq_x.max(), freq_y.min(), freq_y.max()))
count += 1
plt.suptitle('Square filter')
plt.tight_layout()
# Square blur
count = 1
for a in range(1, 25, 5):
sfilt = square_kernel(rotim.shape, a=a)
plt.subplot(2, 3, count)
plt.imshow(np.abs(np.fft.ifft2(np.fft.ifftshift(sfilt*rotim))))
count += 1
plt.suptitle('Square filter smoothing')
plt.tight_layout()